In science and engineering, when we have a number of data points obtained by sampling and experimentation, it is possible to construct a function that closely fits those data points. Interpolation can be regarded as a special case of curve fitting, in which the function must go exactly through every single data point.

Estimating the size of a mineral field available for extraction using exploration results, calculating the estimated amount of mineral contained within the field are the domain of reserve mineral estimation. Numerical interpolation algorithms provide a way to maximize the knowledge of known ore occurrences and the method of their formation and determine potential areas where the particular class of ore deposit being sought may exist.

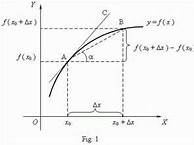
There are various techniques for the solution of interpolation problems and here at Keystone Mining Post will show methods using Cubic Spline and Newton Divided Difference interpolations. These methods are based on Taylor series expansion of a function of f(x) about a specific value of x₀.

Please select from the menu  →    INTERPOLATION APPLICATIONS  (press to select)